[TOC]

起因

今天遇到一个问题，角色卡在一个模型边上，在PVD看模型也比较正常。最终原因呢是因为模型的一个三角形的两个顶点非常进，结果在浮点数运算的时候这种非常小的差异就被丢掉了，所以在PhysX中会判定移动了距离为0的位置，所以一直就卡在原地，跳也跳不起来。来看下两个顶点的信息：

	[0] = {x = -4.10000086, y = -0.200000167, z = -3.56512594}
	[1] = {x = -4.10000086, y = -0.200000077, z = -3.56512594}

只有y值有一丁点的差异，这个时候起码还在浮点数的有效范围内。带上几个问题对研究这个问题会有帮助：

1.为什么 -0.200000167和 -0.200000077浮点数表示不一样，最后加上4.76143503(运算用到的一个坐标)结果就一样了？是什么原因？
2.浮点数运算的逻辑是什么？
3.浮点数的精度为什么是7位？

浮点数的精度

IEEE754表示

IEEE754标准

测试

把上面出问题的数据抽出来测试以下

	float y = 4.76143503;
	float y1 = -0.200000167;
	float y2 = -0.200000077;
	
	float y1Add = y + y1;
	float y2Add = y + y2;
	
	std::cout << std::bitset<32>(*(_ULonglong*)&y) << std::endl;
	std::cout << std::bitset<32>(*(_ULonglong*)&y1) << std::endl;
	std::cout << std::bitset<32>(*(_ULonglong*)&y1Add) << std::endl;
	
	std::cout << std::bitset<32>(*(_ULonglong*)&y2) << std::endl;
	std::cout << std::bitset<32>(*(_ULonglong*)&y2Add) << std::endl;

	cout << "fTest = " << y1Add << endl;
	cout << "fTest1 = " << y2Add << endl;

结果可以看到：

	01000000100110000101110110101101
	10111110010011001100110011011000
	01000000100100011111011101000110
	10111110010011001100110011010010
	01000000100100011111011101000110
	fTest = 4.56143
	fTest1 = 4.56143

小结：

y1和y2的浮点数表示的确不一样，即IEEE754的23位小数位是满足条件的
做了加法之后，结果变成一样了

那么接下来根据问题来分析原因是什么样的。

浮点数运算

参考[2]，[3]的主要步骤：

1.规格化表示
2.对阶
3.尾数标数
4.规格化
5.舍入

	IEEE 754 standard floating point Addition Algorithm
	Floating-point addition is more complex than multiplication, brief overview of floating point addition algorithm have been explained below
	X3 = X1 + X2
	X3 = (M1 x 2E1) +/- (M2 x 2E2)
	1) X1 and X2 can only be added if the exponents are the same i.e E1=E2.
	2) We assume that X1 has the larger absolute value of the 2 numbers. Absolute value of of X1 should be greater than absolute value of X2, else swap the values such that Abs(X1) is greater than Abs(X2).
Abs(X1) > Abs(X2).
	3) Initial value of the exponent should be the larger of the 2 numbers, since we know exponent of X1 will be bigger , hence Initial exponent result E3 = E1.
	4) Calculate the exponent's difference i.e. Exp_diff = (E1-E2).
	5) Left shift the decimal point of mantissa (M2) by the exponent difference. Now the exponents of both X1 and X2 are same.
	6) Compute the sum/difference of the mantissas depending on the sign bit S1 and S2.
If signs of X1 and X2 are equal (S1 == S2) then add the mantissas
If signs of X1 and X2 are not equal (S1 != S2) then subtract the mantissas
	7) Normalize the resultant mantissa (M3) if needed. (1.m3 format) and the initial exponent result E3=E1 needs to be adjusted according to the normalization of mantissa.
	8) If any of the operands is infinity or if (E3>Emax) , overflow has occurred ,the output should be set to infinity. If(E3 < Emin) then it's a underflow and the output should be set to zero.
	9) Nan's are not supported.

然后，我就自己手动计算了一下：

	01000000100110000101110110101101 = 4.76143503
	阶码：10000001 = 129 - 127 = 2
	尾数：1.00110000101110110101101

	--------------------------------------------------
	10111110010011001100110011011000 = -0.200000167
	阶码：01111100 = 124 - 127 = -3
	尾数：1.10011001100110011011000

	01000000100100011111011101000110 = 4.56143475 = 4.76143503 + -0.200000167
	阶码：10000001 = 129 - 127 = 2
	尾数：1.00100011111011101000110

	加法运算：
	1.1001 1001 1001 1001 1011 000
	对齐：小数点左移2-(-3) = 5位
 	0.00001.1001 1001 1001 1001 1011 000
	相减：
	 	1.0011 0000 1011 1011 0101 101
	-	1.0000 1100 1100 1100 1100 110  11 000
	= 	1.0010 0011 1110 1110 1000 111
	比较	1.0010 0011 1110 1110 1000 110

	--------------------------------------------------
	10111110010011001100110011010010 = -0.200000077
	阶码：01111100 = 124 - 127 = -3
	尾数：1.10011001100110011010010

	01000000100100011111011101000110 = 4.56143475 = 4.76143503 + -0.200000077
	阶码：10000001 = 129 - 127 = 2
	尾数：1.00100011111011101000110
	
	加法运算：
	1.10011001100110011010010
	对齐：小数点左移2-(-3) = 5位
 	0.0000110011001100110011010010
	相减：计算器去掉小数点和前面的1来的比较快
	 	1.0011 0000 1011 1011 0101 101
	-	0.0000 1100 1100 1100 1100 110	10010
	=	1.0010 0011 1110 1110 1000 111
	比较	1.0010 0011 1110 1110 1000 110

小结：

计算的结果的确是一样的，但是和最终的4.76143503还是有点不一样（最后一个比特位），这说明我手动计算和机器计算还是有点区别，包括后面的规格化，舍入我就没去细看了，留个问题在这里吧

	// 4.76143503 + -0.200000167
	1.0010 0011 1110 1110 1000 111
	// 4.76143503 + -0.200000077
	1.0010 0011 1110 1110 1000 111
	// 最终结果的二进制
	1.0010 0011 1110 1110 1000 110

这里解释了前两个问题：最主要是在浮点数的运算过程中(这里是加法)，因为要对齐阶码，所以更小的数字的尾数后面几位（这里是5位）都忽略掉了，所以-0.200000167和 -0.200000077的差异也就没有了

再来看看IEEE754有23位小数，为什么精度是7位小数位？

浮点数精度

先确定下自己的问题：

精度指的是十进制的小数点后面的个数，而IEEE754标准的23位指的是二进制有效位
我想理解的是23位二进制有效位是如何换算到十进制的7位有效位的
网上搜索了之后，最终可以确定的是十进制小数点后面可以精确到6-7位
自己最终问题是如何用数学方法证明?

最常见的解释如下，参考[5][6]：

因为float类型的数值由二进制下的后23位决定的，而这后23位表示的十进制的数最大为2^23=8388608，也就是说在二进制下能表示的准确的23位的数转换到十进制下最大的数是7位的，数值是多少不重要，因为这个数是在十进制下是7位，所以float在十进制下的精度位7位。再说白一点，二进制下能表示的最大的准确的数值转换为十进制是7位。

简单来讲，就是二进制可以表示的8388608是一个7位数字，但是并不能包括完全包括所有7位有效位，所以是6-7位有效位。但是，这里我还是有疑问的，这个算法应该是小数点前面可以这么算，小数点后面怎么算的，如果可以这么算，又如何解释？

我的理解

参考[7][8][12]之后，相对而言，我比较喜欢[8][12]的解释。但最终我自己理解又是另外一个。

1.小数点后面的二进制和十进制转换应该是这样的表达式，当然应该要乘以一个0或者1表示有效位上面有数据

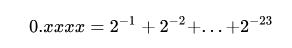
float binary

$0.xxxx = 2^{-1} + 2^{-2} + ... + 2^{-23}$ 那么，小数点后面最小的单位是$2^{-23} = $ 这里其实也说明了浮点数的有些数值只能是近似表示的

2.[8]数学推导

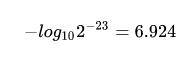
digit precision

\[-{log_{10}}{2^{-23}} = 6.924\]

自己的理解

(1)23位小数，能表示的最小小数位，其他的小数都是乘以这个最小单位构成的[12]

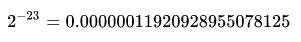
float smallest unit

\[2^{-23}= 0.00000011920928955078125\]

一开始我想，这后面明显有这么多小数，为什么是7位？

(2)这个最小单位表示的就是精度的尾数，怎么理解！如果最小单位是0.1，那么精度就是小数点后面1位，因为你永远也组合不了0.1后面的小数(整数个最小单位求和)，比如0.01、0.02等如果最小单位是0.000001，那么精度就是小数点后面6位，同样的你也永远组合不了0.000001更小单位的小数，比如0.0000001、0.0000002等等
(3)准确来说二进制23位有效位表示的精度为小数点后面6~7位。由上面一条可以知道，0.00000011920928955078125这个最小单位用23位二进制任意组合(求最小单位的倍数)，只能得到比这个0.00000011920928955078125更大的数。所以永远得不到0.00000001这样的小数（精度为小数点后面8位），但是肯定可以得到0.000001（精度为小数点后面6位）的小数。但是不能完全表示精度位小数点后面为7位的小数。下面忽略舍入的算法，只取小数点后面7位有效位的计算结果：
```
0.00000011920928955078125 * 1 = 0.0000001
0.00000011920928955078125 * 2 = 0.0000002
0.00000011920928955078125 * 3 = 0.0000003
0.00000011920928955078125 * 4 = 0.0000004
0.00000011920928955078125 * 5 = 0.0000005
0.00000011920928955078125 * 6 = 0.0000007
0.00000011920928955078125 * 7 = 0.0000008
0.00000011920928955078125 * 8 = 0.0000009
0.00000011920928955078125 * 9 = 0.000001
```
可以看到0.0000006表示不出来，如果考虑舍入的话可能是其他的表示不出来，所以说不能完全表示所有的小数点后面7位小数