[TOC]

最近遇到一个问题，模型上面的一个骨骼因为模型缩放之后它的变换矩阵各种不对。搞得有点迷糊，所以这里记录一下

矩阵变换

已知下面这样的变换

\[M_{BoneLocal} * M_{Local->World} = M_{BoneWorld}\]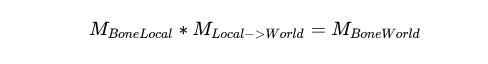

MatrixBone2World

其中，$M_{Local->World} = M_{Model}$

测试UE4

Cylinder和Cone是父子关系

父子关系

圆柱体的变换矩阵

圆柱体变换矩阵

圆锥的变换矩阵

圆锥变换矩阵

解除父子关系圆锥的坐标从缩放1.5前后如下

缩放前世界坐标系变换矩阵缩放后世界坐标系变换矩阵

小结：

可以看到子物体在世界坐标系的变换矩阵是有缩放信息，并且坐标也是缩放过后的
写个简单的代码测试一下，也是这样的结果

    XMMATRIX xmModelScale = XMMatrixScaling(1.0f, 1.0f, 1.0f);
    XMMATRIX xmModelTrans = XMMatrixTranslation(0.0f, 100.0f, 100.0f);
    XMMATRIX xmModel = XMMatrixMultiply(xmModelScale, xmModelTrans);
    XMFLOAT4X4 f4x4Model;
    XMStoreFloat4x4(&f4x4Model, xmModel);

    XMMATRIX xmLocalTrans = XMMatrixTranslation(0.0f, 0.0f, 200.0f);
    XMMATRIX xmBone = XMMatrixMultiply(xmLocalTrans, xmModel);
    XMFLOAT4X4 f4x4Bone;
    XMStoreFloat4x4(&f4x4Bone, xmBone);

    xmModelScale = XMMatrixScaling(1.5f, 1.5f, 1.5f);
    xmModel = XMMatrixMultiply(xmModelScale, xmModelTrans);
    xmBone = XMMatrixMultiply(xmLocalTrans, xmModel);
    XMStoreFloat4x4(&f4x4Bone, xmBone);

测试结果：

模型缩放的错误想法

模型缩放之后，公式中的$M_{Local->World} $是带了缩放的。但是一开始的想法是把原来的矩阵乘以一个新缩放矩阵就可以了： $M_{Model_New} = M_{Model} * M_R$

MatrixNewError

但是，在代码里面这里明显不对，所以一直不理解！

把书翻了一遍，看DX11里面介绍组合变换是：$M = SRT$

新的理解如下：

$M=SRT$可以看出来变换矩阵是已经包含了缩放、旋转和平移。而且，顺序很重要，下一小节单独再分析下
但是我上面的想法是相当于变换了两次，两个矩阵里面都有缩放、旋转、平移。这样最重要的一点是：第二次以为的缩放会把前一个矩阵的位置信息给缩放了!这也是我很疑惑为什么把缩放矩阵放在前面$M_{Model_New} = M_R*M_{Model}$这样是对的。其实不完全是，这样写，是两次变换！但是为什么是对的，只是相当于乘了两个缩放而已$M=SSRT$，并且后面一个缩放矩阵刚好是单位矩阵这么巧罢了。

所以，一般做法是拿到缩放、旋转和平移的分量，然后再构造新的矩阵

                  XMMATRIX matAnimActorWorld = XMMatrixTransformation(
                      g_XMZero,
                      g_XMIdentityR3,
                      g_XMOne,
                      g_XMZero,
                      XMLoadFloat4(&f4AnimActorRotation),
                      XMLoadFloat3(&f3AnimActorPosition)
                  );

旋转顺序

很多地方可以看到$M=SRT$表示的是缩放->旋转->平移这样的顺序，这个顺序很重要，为社么？至于OpenGL里面的顺序是反的，只是矩阵的行列不一样，就不多说了

参考[2]提到了重要的原因是，这些变换是针对坐标系原点来的！

DX11里面的经典的图图(a)先旋转再平移，图(b)先平移再选装

自己测试

  XMMATRIX skullScale = XMMatrixScaling(0.5f, 0.5f, 0.5f);
  XMMATRIX skullOffset = XMMatrixTranslation(0.0f, 1.0f, 0.0f);
  XMStoreFloat4x4(&mSkullWorld, XMMatrixMultiply(skullScale, skullOffset));

M=RT M=RT

M=TR：可以看到相对于原点缩放，先平移之后，原点缩一半就下降了一半 M=TR

问题解决

再来解决遇到的问题，已知模型缩放前的世界坐标系的变换矩阵$M_{Model}$，和骨骼的世界坐标系的变换矩阵$M_{BoneWorld}$，现在模型有缩放，如何求骨骼的新的世界坐标系的变换？

(1)求出Local矩阵

\[M_{BoneLocal} = M_{BoneWorld} * {M_{Local->World}}^{-1} = M_{BoneWorld} * {M_Model}^{-1}\]

(2)重新构造缩放后的矩阵，把$M=SRT$中的S修改成新的缩放因数

\[M_{ModelNew} = M_{Model}重新构造，把缩放值单独算出来\]

(3)用公式算出Bone在世界坐标系的变换矩阵

\[M_{BoneWorldNew} = M_{BoneLocal} * M_{ModelNew}\]

Step

代码问题

这里面的一开始的matModelMatrix是Bone上面的零件在Bone上面的变换矩阵，公式就变成了：$M_{World} = M_{Local1} * M_{BoneLocal} * M_{Model}$ 之前写的一份功能生效的代码：

                    XMMATRIX matWorldInverse = XMMatrixInverse(NULL, matAnimActorWorld);
                    XMMATRIX mat = XMLoadFloat4x4(&f4x4BoneMatrix);
                    mat = XMMatrixMultiply(mat, matWorldInverse);
                    XMStoreFloat4x4(&f4x4BoneMatrix, mat);

                    XMVECTOR xTrans, xScaling, xRotation;
                    XMFLOAT3 f3Scaling;
                    XMFLOAT4 f4Trans;
                    XMMatrixDecompose(&xScaling, &xRotation, &xTrans, XMLoadFloat4x4(&f4x4BoneMatrix));

                    XMStoreFloat4((XMFLOAT4*)&f4Trans, xTrans);
                    f4Trans.x = f4Trans.x * fRenderScale;
                    f4Trans.y = f4Trans.y * fRenderScale;
                    f4Trans.z = f4Trans.z * fRenderScale;

                    XMStoreFloat4x4(&f4x4BoneMatrix,
                        XMMatrixAffineTransformation(xScaling, g_XMZero, xRotation, XMLoadFloat4(&f4Trans)));
                    matModelMatrix = XMMatrixMultiply(matModelMatrix, XMMatrixMultiply(XMLoadFloat4x4(&f4x4BoneMatrix), matAnimActorWorld));
                    XMStoreFloat4x4(&f4x4BoneMatrix, matModelMatrix);

所以就是零件->Bone->世界坐标系：

\[M_{World} = M_{Local1} * M_{BoneLocalNew} * M_{Model}\]

MatrixMore

其中后面两个矩阵相乘相当于：$M = M1*M2=S_1R_1T_1 * S_2R_2T_2$，而代码里面是直接把M1的位移缩放了，这样的结果就是最终的矩阵的坐标是对的，但是缩放信息没有带出来。正确的写法：

                    XMMatrixDecompose(&xScaling, &xRotation, &xTrans, matAnimActorWorld);
                    XMStoreFloat3((XMFLOAT3*)&f3Scaling, xScaling);
                    f3Scaling.x = f3Scaling.x * fRenderScale;
                    f3Scaling.y = f3Scaling.y * fRenderScale;
                    f3Scaling.z = f3Scaling.z * fRenderScale;
                    matAnimActorWorld = XMMatrixAffineTransformation(XMLoadFloat3(&f3Scaling), g_XMZero, xRotation, xTrans);
                    matModelMatrix = XMMatrixMultiply(matModelMatrix, XMMatrixMultiply(mat, matAnimActorWorld));

另外一种写法的错误

                    XMVECTOR xTrans, xScaling, xRotation;
                    XMFLOAT3 f3Scaling;
                    XMFLOAT4 f4Trans;
                    XMMatrixDecompose(&xScaling, &xRotation, &xTrans, matBone);
                    XMStoreFloat3((XMFLOAT3*)&f3Scaling, xScaling);
                    f3Scaling.x = f3Scaling.x * m_fRenderScale;
                    f3Scaling.y = f3Scaling.y * m_fRenderScale;
                    f3Scaling.z = f3Scaling.z * m_fRenderScale;

                    XMStoreFloat4((XMFLOAT4*)&f4Trans, xTrans);
                    f4Trans.x = f4Trans.x * m_fRenderScale;
                    f4Trans.y = f4Trans.y * m_fRenderScale;
                    f4Trans.z = f4Trans.z * m_fRenderScale;

                    matBone = XMMatrixAffineTransformation(XMLoadFloat3(&f3Scaling), g_XMZero, xRotation, XMLoadFloat4(&f4Trans));

相当于把$M = M1M2=S_1R_1T_1 * S_2R_2T_2$中的$T_1S_2$做了，并且S_2是单位矩阵。所以呢？虽然大部分时候都是对的，但是如果模型原来的缩放不是单位矩阵，比如缩放0.5，你现在要放大1.5，那么就bug了

参考

[1]物惯(子到父节点）变换顺序原因和不同坐标系下的变换顺序详解

[2]为什么转换顺序非常重要

矩阵变换的一次释疑

矩阵变换

模型缩放的错误想法

旋转顺序

问题解决

参考

Similar Posts

Comments