[toc]
在做作业的时候,发现和很多其他同学遇到一样的问题:旋转了90°。在作业3的小牛的时候,倒立的图像实在是看不过去了,就打算回头来研究一下这个问题了
学习
- 原因
参考[1][2],先说一下问题原因:代码里面传过来的近平面和远平面都是正数,但是在课程视频里面说的n, f都是负数,看范围也可以看出来是是要写成[f, n]。
- 解决
看了一下参考[1][2]中一些同学说的方法,把正负取反,以及乘以一个变换矩阵,都觉得怪怪的,所以手动推导一遍投影矩阵,直接应用这个公式看看。
透视投影矩阵推导
一些设定
###
- 坐标系:右手坐标系
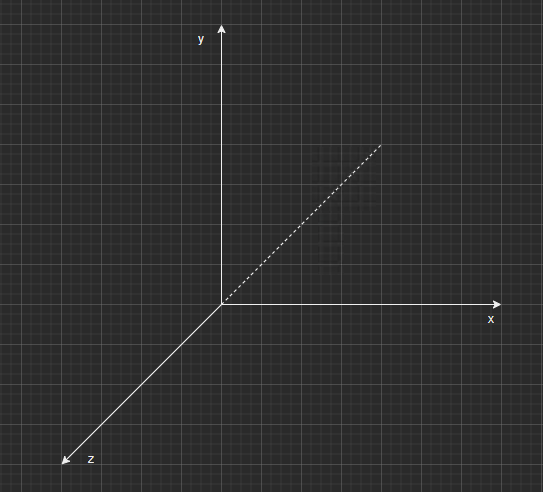
###
- 向量记法:列向量
- 摄像机是在原点,并且朝向z轴负方向看
这个会导致空间中任意一个要归一化标准立方体的范围是[l,r]x[b,t]x[f,n]
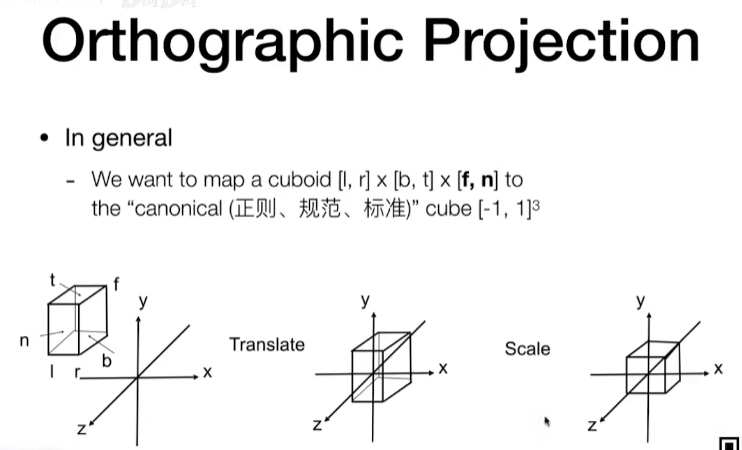
推导过程
简单思路就是,先把透视投影矩阵转换到正交投影矩阵
- 正交投影矩阵
直接参考视频《Lecture 04 Transform Cont.》。先平移再缩放,这里因为是列向量表示法,所以是缩放矩阵x平移矩阵。
\[M_{ortho} = \begin{bmatrix} \dfrac{2}{r-l} & 0 & 0 & 0 \\ 0 & \dfrac{2}{t-b} & 0 & 0 \\ 0 & 0 & \dfrac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\dfrac{r+l}{2} \\ 0 & 1 & 0 & -\dfrac{t+b}{2} \\ 0 & 0 & 1 & -\dfrac{n+f}{2} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\]- 齐次坐标空间性质
对于3D空间中任意一点(x, y, z),其次坐标乘以任意一个非0的实数都表示的是3D空间中的同一个点。即(x, y, z, 1) == (xz, yz, z^2, z != 0),这里乘以特殊的z也是满足这个性质的。
- 透视投影视锥体上点投影到正交投影的立方体上 对于任意一点(x, y, z)投影到(x’, y’, z’)
- y->y’
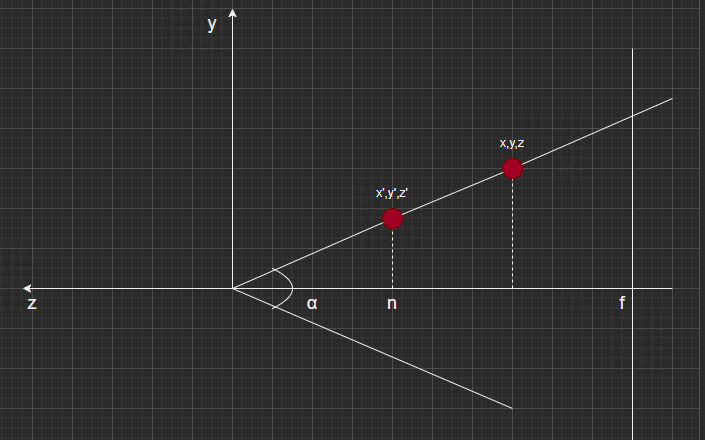
可以很容易求出来(相似三角形)
\[y' = \dfrac{n}{z}y\]- x->x’
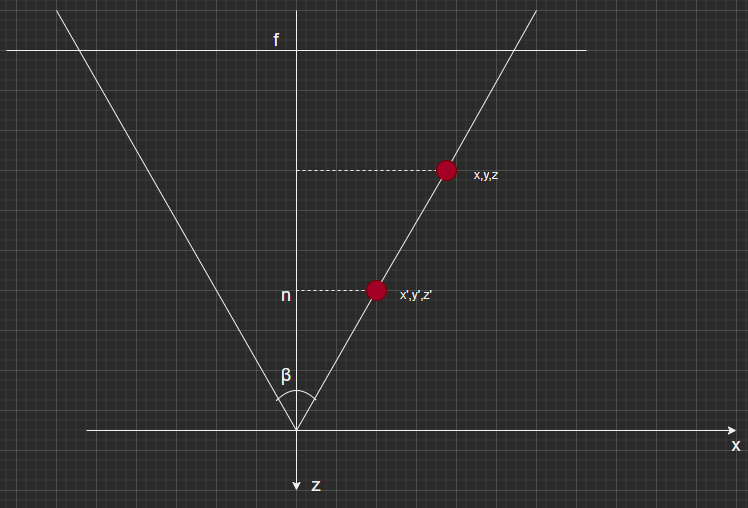
同理可得
\[x' = \dfrac{n}{z}x\]- 根据其次坐标空间性质,变换后的点都乘以z
现在z不知道,接下来构建矩阵
\[M_{persp->ortho} \begin{pmatrix} x \\ y \\ z \\ 1 \\ \end{pmatrix} = \begin{pmatrix} nx/z \\ ny/z \\ ? \\ z \\ \end{pmatrix} = \begin{pmatrix} nx \\ ny \\ ? \\ z \\ \end{pmatrix}\]- 初步可得
- 根据两个特例来求上面这个矩阵
(1)对于近平面上的点,变换前后没有任何变化
(2)对于远平面上的中心点,变换前后没有变换
- 近平面上的点满足条件
\(M_{persp->ortho} \begin{pmatrix} x \\ y \\ n \\ 1 \\ \end{pmatrix} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{pmatrix} x \\ y \\ n \\ 1 \\ \end{pmatrix} = \begin{pmatrix} x \\ y \\ n \\ 1 \\ \end{pmatrix}== \begin{pmatrix} nx \\ ny \\ n^2 \\ n \\ \end{pmatrix}\) 可知第三行前面两个和xy无关,但是可能和后面两个有关,设为A和B。所以矩阵可以写成如下形式:
\(M_{persp->ortho} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & A & B \\ 0 & 0 & 1 & 0 \\ \end{bmatrix}\) 可得第一个等式
\[An + B = n^2\]- 对于远平面中心点
可得第二个等式
\[Af + B = f^2\]根据两个等式可分别求得A和B:
\[\begin{aligned} & A = n + f \\ & B = -nf \\ \end{aligned}\]- 先列出来fov和n的关系
因为f < n < 0,所以:
\[\begin{aligned} & tan(β/2) = \dfrac{ratio}{-n} \\ & tan(α/2) = \dfrac{1}{-n} \\ \end{aligned}\]其中:
\[\begin{aligned} & h = 1 \\ & ratio = \dfrac{w}{h} = w \end{aligned}\]参考《3D Game Programming with DirectX 11》这本书里面的推导的概念,因为主要是关心纵横比(aspect ratio),所以可以简化的把h设置为1.
- 正交投影矩阵表示
- 最终的透视投影矩阵
- bingo
这样结果虽然对了,但是其实是不合理的,因为传进来的f > n > 0是和这个推导不一致的。如果把-f, -n 代入到上面的矩阵,结果还是不对。代码里面应该还有哪个地方做了一次转换把这个问题给屏蔽掉了,后面继续看!
扩展
关于推导,看到上面就ok了,但是我在想左手和右手坐标系关系到底有多大,所以打算推一遍左手坐标系的
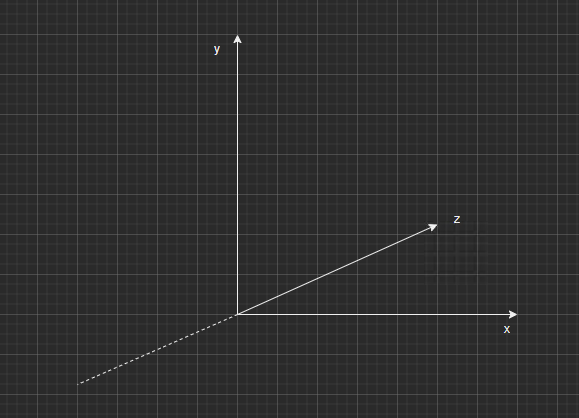
- 行向量表示法
- 摄像机朝向z轴正方向看,立方体表示为[l, r]x[b,t]x[n,f]
注意这里f > n > 0
矩阵推导
- 正交矩阵
- 透视投影矩阵
求出来的A和B跟右手坐标系是一样的结果:
\[\begin{aligned} & A = n + f \\ & B = -nf \\ \end{aligned}\]从这里可以看出来一点就是透视到正交的变换是跟坐标系无关的
\[\begin{aligned} M_{persp} &= M_{persp->ortho}M_{ortho} \\ &= \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \dfrac{1}{ratio} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \dfrac{2}{f-n} & 0 \\ 0 & 0 & -\dfrac{n+f}{f-n} & 1 \\ \end{bmatrix} \\ & = \begin{bmatrix} \dfrac{n}{ratio} & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & \dfrac{n+f}{f-n} & 1 \\ 0 & 0 & \dfrac{2nf}{f-n} & 0 \\ \end{bmatrix} \\ & = \begin{bmatrix} \dfrac{1}{tan(β/2)} & 0 & 0 & 0 \\ 0 & \dfrac{ration}{tan(β/2)} & 0 & 0 \\ 0 & 0 & \dfrac{n+f}{f-n} & 1 \\ 0 & 0 & \dfrac{2nf}{f-n} & 0 \\ \end{bmatrix} \end{aligned}\]可以看到这里和《3D数学基础图形与游戏开发》这本书上的是一样的
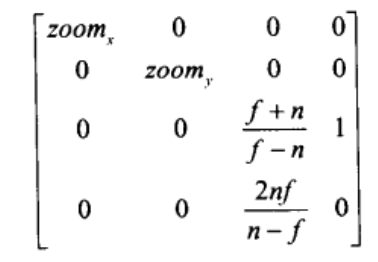
疑问:《3D Game Programming with DirectX 11》不一样是为什么?
书上推导出来的矩阵形式如下:
\[\begin{bmatrix} \dfrac{1}{rtan(α/2)} & 0 & 0 & 0 \\ 0 & \dfrac{1}{tan(α/2)} & 0 & 0 \\ 0 & 0 & \dfrac{f}{f-n} & 1 \\ 0 & 0 & -\dfrac{nf}{f-n} & 0 \\ \end{bmatrix}\]参考书上5.6.3.4章节
- 原因
原因主要是DX里面要求的立方体在z轴方向的范围是[0,1],而不是这里的[-1,1]。所以,把上面的正交投影矩阵改一下即可
- 正交投影矩阵
- 透视投影矩阵
这样就和书上一致了。
参考
[1]https://zhuanlan.zhihu.com/p/509902950
[2]https://games-cn.org/forums/forum/graphics-intro/page/3/
[3]https://www.bilibili.com/video/BV1X7411F744?p=4&vd_source=c10ae5c27bbde8ef3af23889645a0d8b
[4]《3D Game Programming with DirectX 11》
[5]《3D数学基础图形与游戏开发》